2023/05/31

算数・数学のよいところ

松野陽一郎

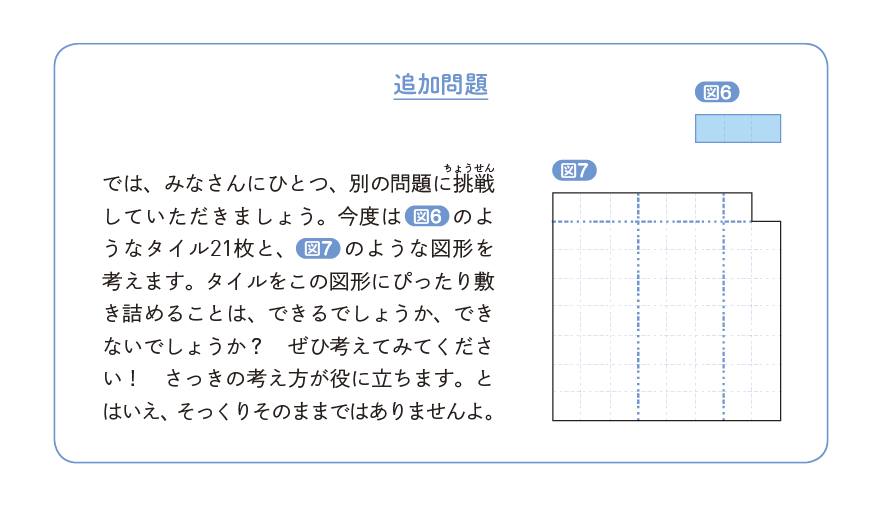
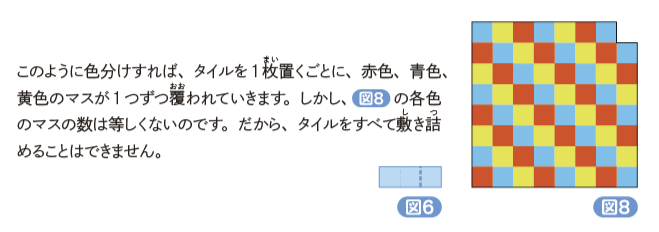
　皆みなさんは、算数・数学を、どんなものだと感じていますか。私わたしもずいぶん長い間、算数や数学とつき合っていますが、いまだに、「こういうものです」と一言で言うことはできないでいます。よいものであるとは感じていますが、語りだすとどうにもまとまらないのです。
　ここでは、考えるきっかけになるように、このページ数で話せる算数・数学の問題（と少しのおまけ）を以下に用意しました。ぜひ、考えてみてください。

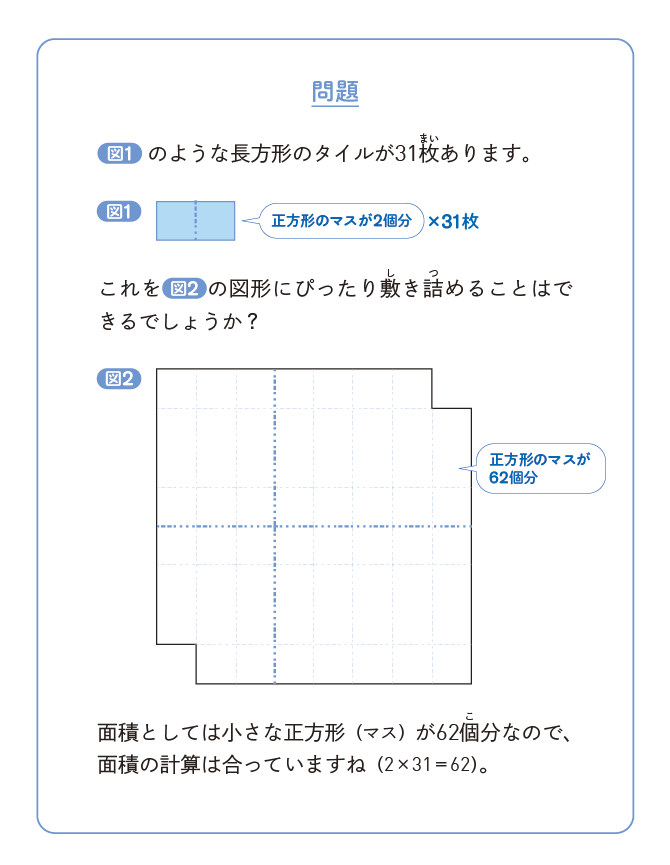
　こんなに広いところに小さいものを詰めていくので、どうにでもなりそうな感じがしますね。そこで端はしから思いつくままにタイルを置いていくと......おや、置くほどに制せい限げんがきつくなり......どうしても長方形のタイルを置けない場所ができてしまいます（図３・図４）。

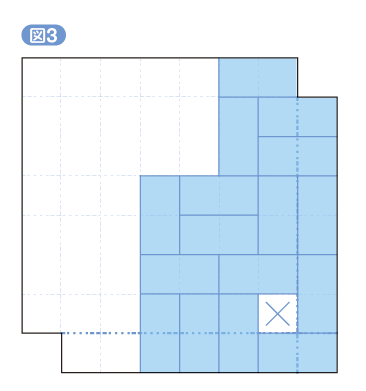
　しかし、一回や二回失敗したところで、「こんなの絶ぜっ対たいできない」とあきらめるわけにはいきません。「ほかにもっとうまいやり方があるかも」と、もっとがんばってみるのが当然だと思いますが、いくらやってもうまくいきません。......などと私が自信たっぷりに言いきるのは、何かからくりがありそうですね。実は、どれほど工夫してタイルを置いていったとしても、きれいに敷き詰めることは絶対にできません。

　なぜでしょうか？　いきなり結けつ論ろんだけ言われても、すぐ信じる気にはなれませんね。誰だれもが納なっ得とくできる論理をもとに、誰にもわかるように説明されたことだけが、数学では正しいと認みとめられます。
　この問題には、短くて明めい快かいなとてもよい説明があるので、それを紹しょう介かいしましょう。
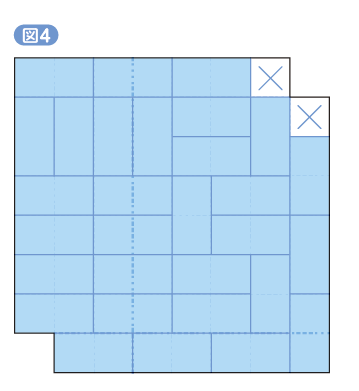
　まずは、図２の62マスの正方形を、互たがい違ちがいに塗ぬり分けるのです（図5）。このような模も様ようを市松模様、チェッカー模様などといいます。「鬼き滅めつの刃やいば」で見た人も多いでしょう。

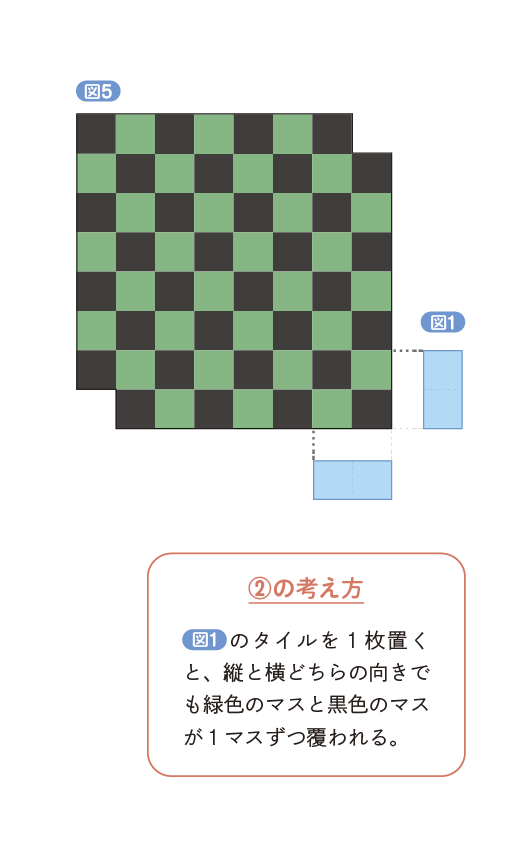
　そして、次の2つのことを考えましょう。これが納得できれば、もうゴールは間近です。

- ① 62マスのうち、緑色のマスは30個、黒色のマスは32個ある。
- ② 図1のタイルをどこに置いたとしても、それで覆おおわれる2つのマスのうち、一方は緑色、他方は黒色である。

　では、①と②を組み合わせて考えてみましょう。図１のタイルは31枚ありました。もし図１のタイルをきれいに敷き詰めることができるとすると、②のことから、緑色のマス、黒色のマスはそれぞれ31個ずつタイルで覆われるはずです。しかしそれは①の「緑色のマスは30個、黒色のマスは32個ある」ことと話が合いません（「矛む盾じゅんが生しょうじる」といいます。「矛盾」はつじつまが合わないことという意味の故こ事じ成せい語ごです）。だから、タイルをぴったり敷き詰めることはできないのです。

　私はこの問題に対するこの説明がとても好きです。その理由をいくつか挙げてみます。みなさんはどう思われるでしょうか。

●タイルを敷き詰めることと一見全然関係なさそうな「市松模様の塗り分け」が解かい決けつに役に立つ意い外がい性せい。「どうしてこんなことを思いつけるんだろう？」と、不思議なものを見たような、わくわくした気持ちになります。
●見た目に納得しやすい。タイルを縦たて向きに置いても横向きに置いても、確たしかに、緑色のマスと黒色のマスを1つずつ占せん領りょうします。これはあまり考えなくても「目で見て」わかります。だからタイルを31枚置けば......と考えを進めるところに、無理がありません。不自然なことを考えなくても解決できるのはとても気分がよいです。
● 一いっ瞬しゅんでわかる。タイルの置き方をあれこれ何度も試ためしてみる、という作業を一いっ切さいしないで説明が完結するのはすごいと思います。何度も敷き詰めるのに失敗し、でも実はうまい置き方があるのかも......と迷まよう心を瞬時に安心させる説明です。論理の力、数学の力を感じさせられます。

　この問題に対する説明は、これしかないわけではありません。地道に場合分けを続けて「敷き詰められない」と結論づけることもできるでしょうし、コンピューターにタイルのあらゆる置き方をすべて調べつくさせるのも立りっ派ぱな説明方法だと思います。しかしそうであっても、ここに紹介した説明のおもしろさ、さわやかさは、やはり抜ばつ群ぐんのものだと思うのです。そしてそれは、私が考える〈算数・数学のよいところ〉ととても深い関係があるように思えるのです。
　みなさんが日ひ頃ごろ学校で向かい合っている算数・数学と、いま私が話したものとは、あまり似にてないと感じるかもしれません。学校での授じゅ業ぎょうは、算数・数学を使いこなせるようになるための基き礎そトレーニングでもあるので、なかなかこのような鮮やかな話ばかりではないでしょう。でも、そんな学校での算数・数学の先には、美しいアイディアとみごとな整合性に満ちあふれた算数・数学があるのです。みなさんにちょっとでも、そんなことを感じていただければ幸いです。